
360 derece, daireyi tanımlayan en temel ifade, nereden geliyor bu 360 derece, neden 360?
Derece’nin tanımı şu şekilde yapılmış: düzlem açının bir ölçüsü. Tam bir daire toplam 360 derece kabul edilmiş. Standart bir birim değil. 1 derece = π/180 radyan olarak hesap edilir. Derece’nin tarihte nereden geldiği bilinmiyor. Eskiden gökbilimciler güneşin hareketinden bulmuş olabilirler. Çünkü geçmişte bir yıl 360 gün olarak kabul ediliyordu. Bu durumda güneş, takip ettiği eliptik yolu her gün bir derece değiştirir. Ayrıca 360 sayısı birçok sayıya bölünebilir. 1’den 10’a kadar olan sayılar içinde sadece 7 sayısına tam olarak bölünemez. Ayrıca Babiller bizim gibi 10 tabanlı sayı sistemini değil, 60 tabanlı sayı sistemini kullanıyorlardı. Onlardan geliyor olabilir. Tam bir daireyi 360 derece kabul etmişler. Diğer bir ölçü birimi olan Radyan 180 /π şeklinde hesaplanır. 1 Radyan 57 dereceden biraz büyüktür. 1 Radyan = 180 /π = 57,29577951…derecedir.
Ulaşılması imkânsız mükemmelliği simgeleyen Daire; çevresinin, çapına oranı olan ve ondalık basamakları kendini tekrar etmeden sonsuza uzanan, matematik dünyasının en gizemli sayısının, yani; π sayının gizemini içinde saklar.
Dairenin olduğu her yerde π sayısı vardır.
π sayının gizemini anlatmaya maalesef kitaplar yetmez.
Asal sayı olarak en küçük ve en yakın tam sayı oranı :
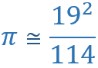
Neden 19 ve 114 ?!! Başka sayı mı kalmadı?!! sorusu geliyor insanın aklına.
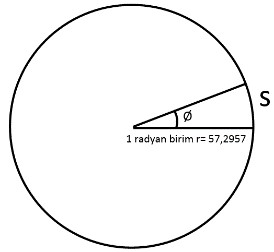
Radyan Çemberi: 1 radyan = 180 ÷ π = 57,29577951…
Çevresinin uzunluğu 360 birim ve Yarı çapı; r = (1 radyan) 57,29577951… birim olan çemberde, merkez açının gördüğü yayın uzunluğu, derece olarak açının değerine eşittir. Ø ̊ = S birim
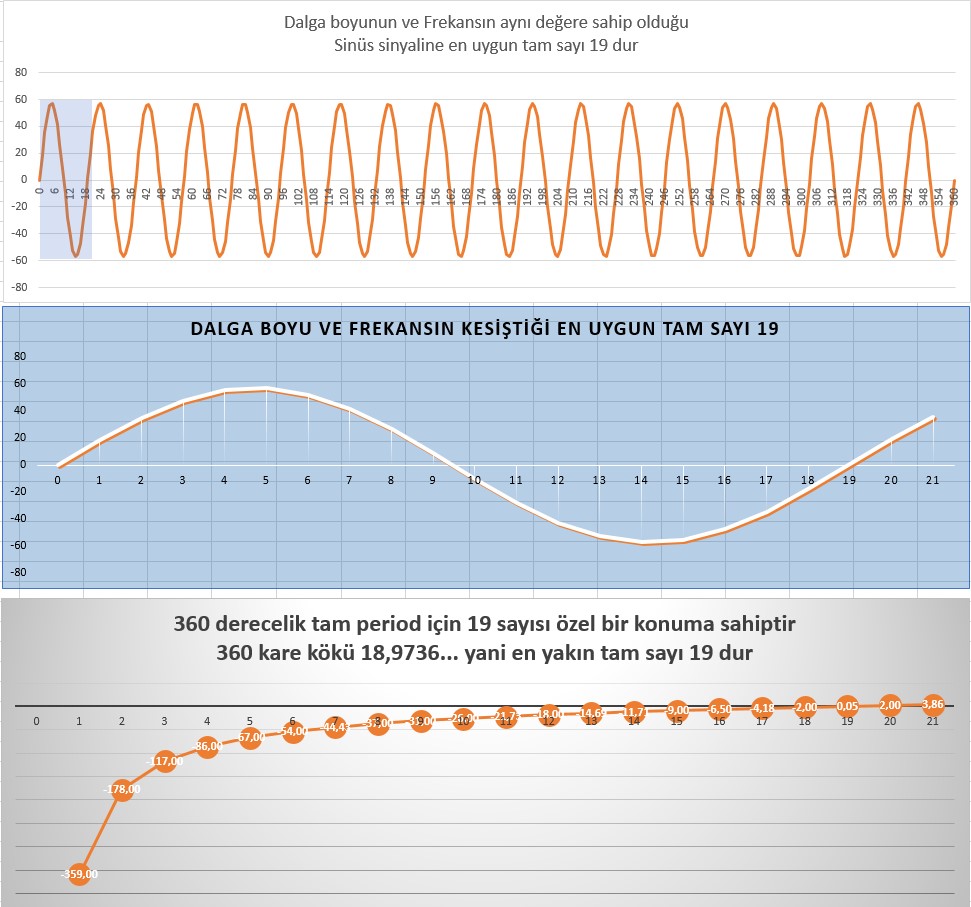
360’ın karekökü 18,97366596… en yakın tam sayı 19 dur.
π = 3,1415926535897932384626433832795…
Dairede mükemmel bir uyum beklentisi içerisinde sınırları zorluyoruz,
Dairenin mükemmel böleni olan
Tam sayıyı veya En yakın tam sayıyı arıyoruz.
Dilim Sayısının
ve
Açı Değerinin
ve
Gördüğü Yay Uzunluğunun
hepsinin birbirine eşit olduğu tam sayıyı
veya
hepsinin birbirine eşit olduğu en yakın tam sayıyı
ve
bu değerle orantılı, yarı çapın ve oradan da çapın değeri olan
TAM SAYIYI ARIYORUZ
veya
EN YAKIN TAMSAYIYI ARIYORUZ
n = Dilim Sayısı = Açı Değeri = Gördüğü Yay Uzunluğu
n = 2 · π · r /n
2 · π · r = 360
n²= 2 · π · r = 360
n²= 2 · π · a · n = 360
denkliğini sağlayan, en yakın tam sayıları, a: kat sayını ve n: dilim sayısını arıyoruz
n²= 360 → n = √360
n = 18,974
Dilim sayısı tam sayı olmak zorunda olduğu için;
en yakın tam sayı olarak dilim sayısı
n ≅ 19
olur
2 · π · a · n = 360 → 2 · π · a · 18,974 = 360 → a = 360/(2 · π · 18,974)
a = 3,019
en yakın tam sayı olarak a katsayısı
a ≅ 3
olur
Dilim sayısı tam sayı olacaktır, fakat Açı değerinin ve Yay uzunluğunun, π sayısının sonsuza giden ondalık basamakları sebebiyle, bu şartları sağlayan tam sayı olması mümkün olmayacaktır. Dolayısıyla Açı değeri ve Yay uzunluğu yaklaşık olarak alınacak en yakın tam sayıya yuvarlanacaklardır. Birbirine eşit olan Açı değeri ve Yay Uzunluğu (19 – 1÷19 = 18,974) olarak hesaplanır. En yakın tam sayıya yuvarlandığında 19 olarak bulunur ve dilim sayısı da 19 olarak karşımıza çıkar. Buradan a katsayısı en yakın tam sayı olarak 3 bulunur. Yine; Açı değerinin ve Yay Uzunluğunun birbirine en yakın olduğu yarı çap uzunluğu, tam sayı olarak 57 birim bulunur. 19 sayısı, yarı çap olan 57 sayısına (19+19+19) ve çap olan 114 sayısına (19+19+19+19+19+19) uyumludur.
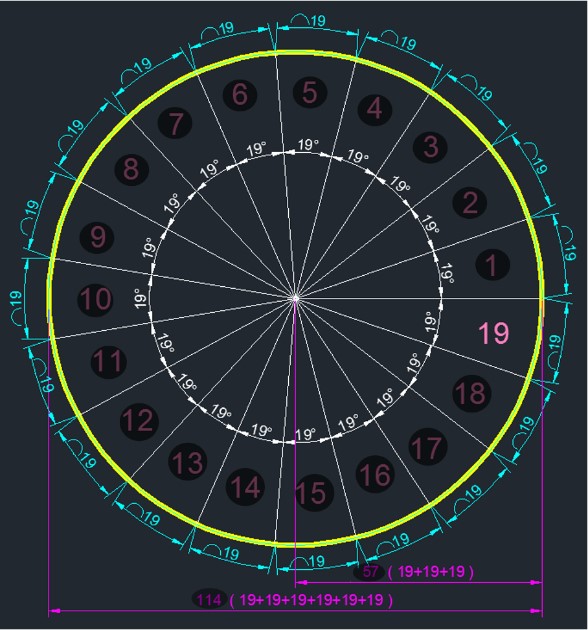
n = 19 , a = 3 , r = 57 , R = 114
n² = 2 · π · a · n = 360
19² ≅ 2 · π · 3 ·19 ≅ 360
Sonuç olarak dairede mükemmel uyumu tam sayı olarak 19 sayısı ile yakalıyoruz
En yakın tam sayıya yuvarlandığında bütün değerler
(Açı değeri, gördüğü Yay uzunluğu, Dilim sayısı, Yarı çap ve Çap değeri)
19 sayısı ile uyumludur.
( 19 – 1÷19 )
Bir dairede, 19 – 1÷19 ≅ 19 derecelik açılar ile tam 19 adet dilim oluşur,
yarıçap uzunluğu 1 radyan = 180 ÷ π = 57,2957 birim olduğunda,
19 dilimin her birinin yay uzunlukları 19 – 1÷19 ≅ 19 birimdir.
360÷19 = (361-1) ÷ 19 = (19×19 – 1) ÷ 19= 19 – 1÷19 = 18,974
Yarıçapı en yakın tam sayıya yuvarlandığında 19 + 19 + 19 = 57 birim olur,
bu durumda çap 19 + 19 + 19 + 19 + 19 + 19 = 114 birim olarak karşımıza çıkar.
19 sayısı,
Mükemmel uyumlu Dairenin
En yakın tam sayı olarak
Ortak Bölenidir
Bu yapı tektir, sadece bu sayılarla oluşabilir ?!!;
En yakın tam sayı olarak
yarıçapı 57 birim, çapı 114 birim olan dairede ortaya çıkar
ve
19 tam sayısıyla oluşur.
Bu sayılar Kur’ân sayısal yapısıyla birebir örtüşür.
Kur’ân’ın Matematiksel yapısı,
( sure sayısı: 114, simetri sayısı: 57, kodlama sayısı: 19 )
Kur’ân da 114 sure vardır, 57 + 57 olarak simetrik yapıya sahiptir,
(Çift ve Tek Simetri Sistemi).
Kur’ân 19 sayısı ile matematiksel olarak kodlanmıştır, 19 sayısı Kur’ân’ın ortak bölenidir.
Bir başka Kur’ân bağlantısının ise Radyan değerinde ortaya çıktığını hayretle görüyoruz: Kur’ân sayısal yapısının Simetri Merkezi ve mucizelerle dolu olan 57. Surenin, 29 ayeti vardır. Ondalık olarak 2 hassasiyetli 1 radyan değeri ile örtüşür 57,29. Ondalık hassasiyeti 4 olarak alırsak (57,2957), Surenin adı olan EL-Hadid (Demir) kelimesinin ebced değeri 57 de devreye girer. 57 ve 29 sayıları Kur’ân sayısal yapısının çok önemli, belirgin ve merkezi sayılarındandır. 1 Radyan değeri olan 57,29577951… sayısının, Kur’ân’daki sayısal yapısı ile bu şekilde örtüşmesi bence çok manidardır.

π sayı ile ilgili bağlantı:
Yarıçapı 57 birim, çapı 114 birim olan dairede en yakın tam sayı olarak 19 sayısının bu şekilde ortaya çıkması, 114 ve 19 sayısının evrensel bir sabit olan π sayı ile ilgili bağlantısını kurabilmemizi sağlar.
19² ≅ 2 · π · r 19² ≅ 2 · π · 57 19² ≅ 114 · π 19 · 19 ≅ 19 · 6 · π
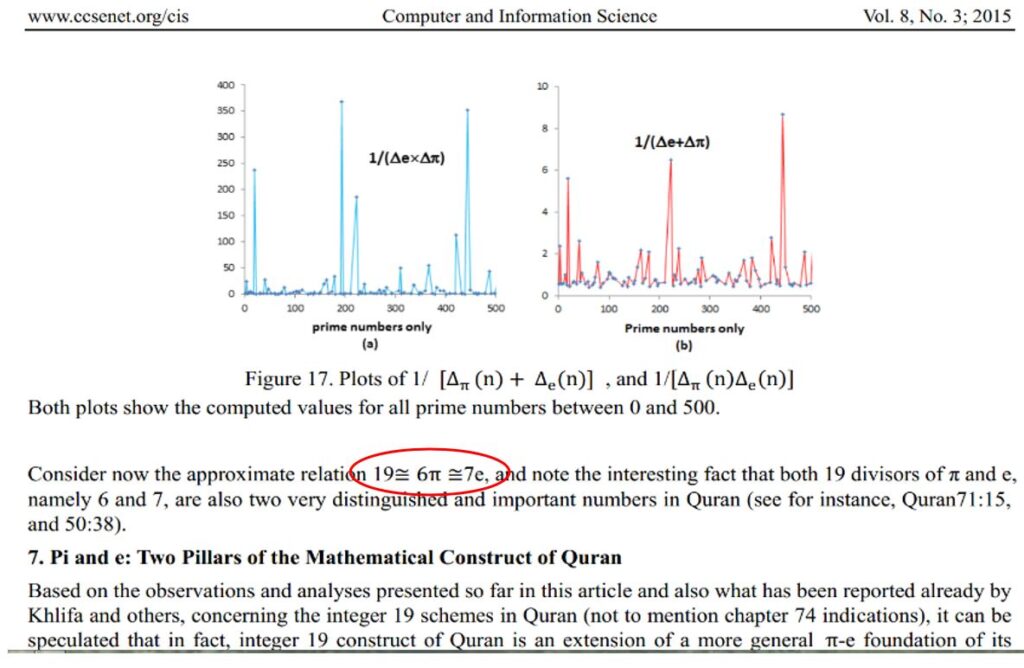
19 ≅ 6π
Bu sonuç Ph.D. Baback Khodadoost’ın çalışmasında başka bir yaklaşımla bulduğu sonuçla aynıdır.
https://pdfs.semanticscholar.org/1c85/c6b669681637f70eb0b7145d4e80ad41fa02.pdf
Bu sonucun bir türevi olarak sinüs sinyalindeki ortaya çıkan durumu meraklısı ile paylaşmak isterim.
1sn’lik zaman dilimini 360 derecelik bir çevrim olarak düşündüm.
Dalga boyunu ise bir dalganın kat ettiği açısal mesafe olarak aldım.


Bir yanıt bırakın