
Kod’un ne olduğunu ve sayısal bilgiden farkını şöyle açıklayabiliriz; Kod sembolik bir ifadedir, sayısal bilgi değildir. Sizin Kredi Kartı numaranız bir Kod’dur, sayı değildir!!! Her gün marketlerden aldığınız ürünlerinde üzerlerinde görebileceğiniz, kasada kolay tanınmasını ve fiyatlanmasını sağlayan barkod’ları mevcuttur. Bu kodlar bir niceliği yani, sayısal büyüklüğü göstermezler. Bir başka ifadeyle, Kredi Kartı numaranız, o kartın kaçıncı kart olduğunu gösteren bir sayı değildir. Aynı şekilde ürün barkodu da o ürünün kaçıncı ürün olduğunu gösteren bir sayı değildir. O kodun içinde değişik anlamlar yüklüdür, ürünün grubu, ürün adı, ürün özellikleri gibi. Ve bu koda bağlı olarak ürünün bütün yapısı tanımlanabilir. Verdiğim ürün kodu örneğinden de anlaşılacağı gibi kod sadece sayılardan oluşmak zorunda değildir, her türlü sembol kullanılarak kod yapılabilir. Bugün hayatımıza girmiş olan birçok kod yapısı endüstride değişik şekillerde kullanılmaktadır.
Kodlama; şifreleme veya kilitleme şeklinde karşımıza çıkar. Kriptoloji olarak ifade edilen bir matematik bilimidir. Kriptoloji, matematiğin hem şifre bilimi (kriptografi), hem de şifre analizini (kriptonaliz) kapsayan dalıdır. Kod ve kodlama kavramlarını iyi tanıdıktan sonra sisteme daha doğru bir anlam yükleme imkânınız vardır.
Kod kelimesi İngilizce şifre anlamına gelen “Code” kelimesinden gelmektedir. Kodlama kelimesi ise şifreleme işleminin yapılmasını ifade eder. İlgilendiğimiz şifreleme türü günümüz teknolojisinde bir mesajın, gizlenmesi, sadece yetkilisi tarafından okunabilmesi veya anlaşılabilmesini sağlamak için metin üzerinde veya gönderilen mesaj üzerinde yapılan çeşitli sayısal uygulamaları içerir. Kelime “Kriptolama” olarak da kullanılmaktadır. Şifreleme sayesinde gönderilen mesaj, sadece elinde anahtar veya şifre bulunan kişiler tarafından çözülebilir ve okunup, anlaşılabilir.
Şifreleme tekniğinin temelinde asal sayılar vardır.
Şifrenin çözülme tekniği ise asal çarpanlara ayırmak ile başlar.
Günümüzde şifreleme konusu “Asal çarpanlara ayırmak: R-S-A Şifreleme” şeklinde ele alınır. RSA şifrelemesi, Ron Rivest, Adi Shamir ve Leonard Adleman tarafından bulunan ve kendi soyadlarının baş harfleri ile isimlendirilmiş açık anahtarlı bir şifreleme yönetimidir. Bir RSA kullanıcısı iki asal sayının çarpımını üretir (19 x 113 = 2147 gibi) ve seçtiği başka bir değerle beraber ortak anahtar olarak ilan eder. Seçilmiş olan asal çarpanları ise saklar. Ortak anahtarı kullanan biri, istediği mesajı istediği gibi şifreleyebilir. Bu yöntemle, eğer ortak anahtar yeterince büyükse sadece asal çarpanları bilen kişi bu mesajı çözebilir. Bilgilerin, verilerin korunmasında güvenlik için kullanılacak asal sayıların olabildiğince fazla basamaklı olması şifrelemeyi daha güçlü yapacaktır. 2009 yılında sonuçlanan bir çalışmada bir grup araştırmacı 232 basamaklı bir sayıyı (RSA-768), yüzlerce makineyi iki yıl boyunca çalıştırarak asal çarpanlarına ayırmışlardır.
25.02.2023 tarihinde yeni eklenen eklenen bölüm:
Kodlama matematiksel bir işlem değildir, hedefi matematiksel bir sonuca ulaşmak değildir. Fakat matematiksel yöntemleri kullanarak hedeflenen sonuca ulaşır. Kodlama veya şifreleme her zaman bir bilginin gizlenmesi için kullanılmak zorunda değildir. Günümüzde birçok değişik alanda kodlamanın değişik amaçlar için kullanıldığını görüyoruz. Konuyu anlamanız için Kredi Kartı Numarasının üretilmesinde ve geçerlilik (benzerlik) kontrolünde kullanılan bir kodlama örneğiyle devam edelim.
Kredi Kartlarının üretilmesinde veya geçerliliğinin kontrolünde, bulan kişinin soyadı ile anılan Luhn algoritması kullanılır. Luhn algoritması, Hans Peter Luhn ve IBM tarafından 1954 yılında geliştirilen bir algoritmadır. Aynı zamanda Luhn Check ve Mod Check olarak da isimlendirilmektedir.
Luhn algoritması 2 şekilde kullanılmaktadır.
1. Yeni bir Kredi Kartı Numarası üretmek yani, verilen bir sayıyı Luhn algoritmasına göre hazırlamak,
2. Verilen bir Kredi Kartı Numarasının geçerli olup olmadığını yani, denkliğini (benzerliğini) kontrol etmek.
Aşağıda Luhn algoritmasının 2. fonksiyonu olan; Verilen bir Kredi Kartı Numarasının Luhn algoritmasına göre geçerli (benzer – denk – misli) olup olmadığının nasıl kontrol edildiğini ve kodlama detayını görmeniz mümkündür.
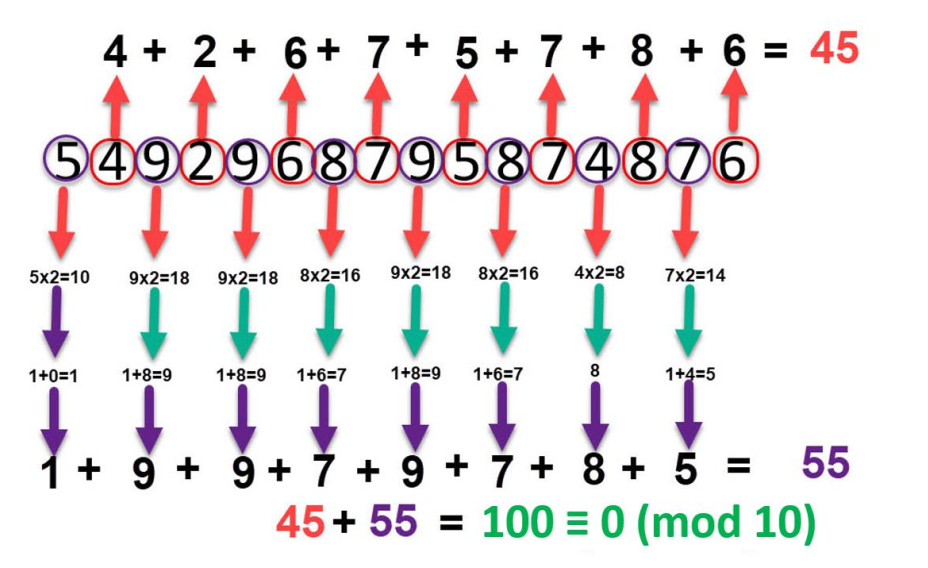
Bu kodlamada, sayılar yan yana yazılmış, belli bir sıradaki sayılar aynı alınmış belli bir diğer sıradaki sayılar 2 sayısı ile çarpılmış ve basamakları toplanarak alınmış ve kodlama üretilmiştir. Geçerlilik kontrolü için ≡ 0 (mod 10) denkliği kullanılıyor. Üretilen kodlamanın bu denkliğin sağlamasıyla, yeni verilmiş olan ve geçerliliği kontrol edilen Kredi Kartı Numarasının Luhn algoritmasıyla üretilen Kredi Kartı Numaraları kümesinin bir elemanı olup olmadığı, yani kümedeki diğer Numaralar ile benzer olup olmadığı tespit edilmiş oluyor. Günümüzde kullanılan tipik bir kodlama örneğidir.
Kur’ân sayısal kodlamasında; kodlamanın mesajı gizlemek için değil, mesajın değiştirilmediğinin görülmesi (fark edilmesi) ve bir benzerinin üretilmesini engellemek için kullanıldığını görüyoruz. Yine günümüz teknolojisinde bu yapı SHA256 algoritması ve Checksum olarak bilinir ve kullanılır. Sayısal kodlamadaki şifrelemenin gücü, metinde ortaya çıkan matematiksel yapının, denkliklerin, eşitliklerin, simetrilerin ve benzerliklerin olasılık değerlerinin birbirine bağlanıp zincir oluşturarak uzamasından kaynaklanır. Olasılık zinciri uzadıkça benzer bir yapının oluşturulması güçleşir hatta imkansızlaşır.
Matematiksel modeli oluşturan kriterlerin birbirlerine bağlantı şeması
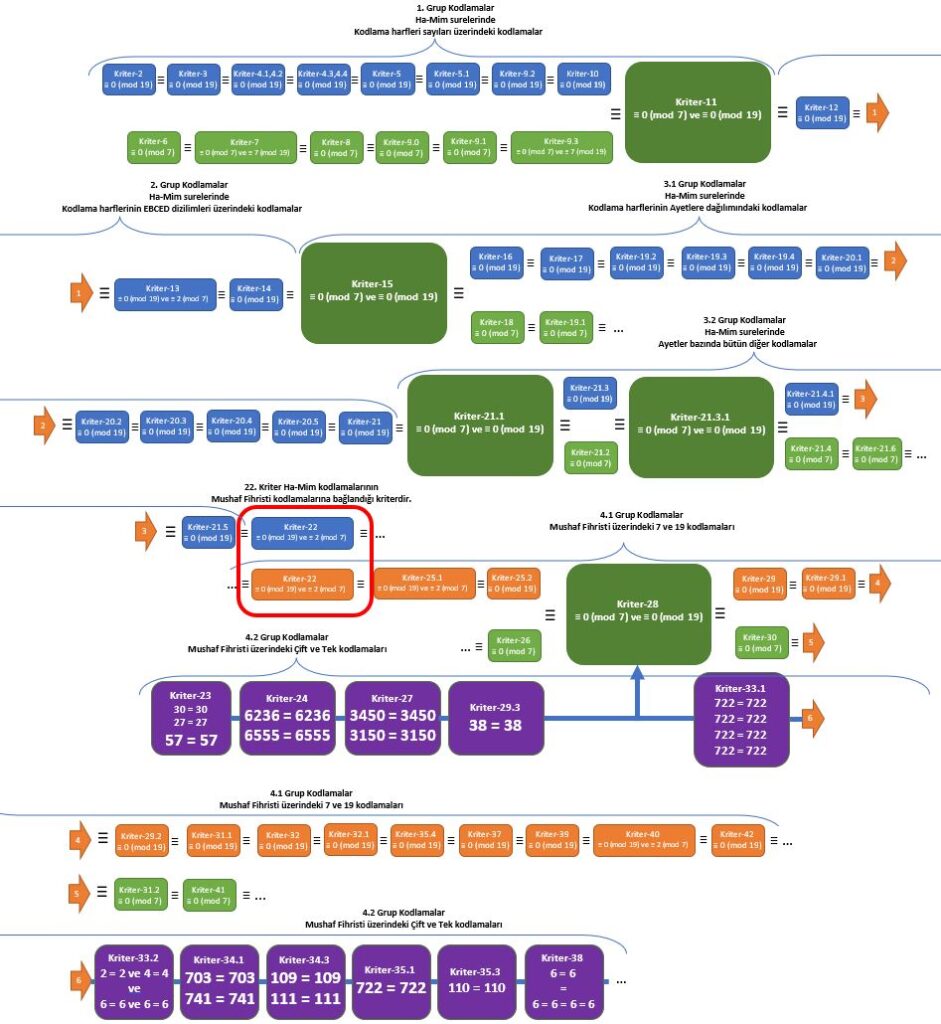
Bir başka ifadeyle, Kur’ân sayısal kodlaması bize mesajın orijinal ve olağanüstü olduğunu gösterir, emin olmamızı sağlar. Sonuç olarak, Kur’ân sayısal kodlamasının belirgin bir bölümü günümüzdeki şifreleme tekniğine benzer şekildedir. Çözümleme için asal çarpanlara ayırma kullanılır.
Asal Çarpanlara Ayırma: Bir doğal sayının asal çarpanlarını bulabilmek için bu doğal sayıyı tam olarak bölünebildiği en küçük asal sayıdan başlayarak sırasıyla asal sayılara bölmemiz gerekir. Nihayetinde sayımızın tam olarak bölünebildiği, bulduğumuz asal sayılar, sayımızın asal çarpanlarını oluşturur. (133 = 7 x 19 266 = 7 x 19 x 2 gibi)
Kur’ân sayısal kodlamasında örgüler (Pattern) bütün detaylarına kadar aynı olmamakla beraber, yapısal olarak birbirlerine benzemektedirler, fakat yinede Kur’ân’da örgüye dayalı sayısal bir kodlamanın genele yayıldığını şimdilik söylemek mümkün gözükmemektedir. Kur’ân üzerinde, geneli kapsayan ve bölgesel olarak görünen birçok sayısal kodlama keşfedilmiştir. Fakat Kur’ân’ın her noktasının, her harf, kelime ve ayetinin sayısal kodlaması benim görüşüme göre, henüz ortaya tam olarak çıkarılamamıştır. Üzerinde çalışmalar devam etmektedir.
Bugüne kadar yapılan çalışmalar sonucunda Kur’ân sayısal kodlamasının kodlama sayılarının, yani genel asal çarpanlarının 7 ve 19 olduğu ortaya çıkmıştır. Matematiksel olarak 7 ve 19 sayıları, 12 kademeli bir çevrimde (mod 12) ikili (El-Mesani) oluştururlar. Bu ifadeyi kolay anlamanız için saat örneğini verebilirim. Çünkü bugün kullandığımız saat sistemi 12 kademeli bir çevrim içerir. Saat 19 dediğimizde saatin akşam 7 olduğunu anlarız.
19 ≡ 7 (mod 12)
7 ve 19 ikili sayısal yapısının hayatımızın nasıl merkezinde olduğunu ve çok ciddi bir fenomen olarak karşımıza çıktığını fark etmemiz gerekir. Odanızın duvarındaki asılı duran duvar saatinize ve takviminize yeni bir bakış açısıyla daha dikkatli bakarsanız, 12 kademeli çevrimi (mod 12) ve 7 kademeli çevrimi (mod 7) orada hemen göreceksiniz. Bir yılda 12 ay vardır ve haftanın günleri 7 gündür. Dolayısıyla 12 kademeli çevrim içinde 7 kademeli çevrimler oluşur. 12 kademeli çevrimde 7 sayısının ikilisi yukarıda izah etmeye çalıştığım gibi 19 dur. Takvimdeki 12 sayısı, Dünyamızın Güneş yörüngesindeki dönüşünden gelir, 7 sayısı ise uydumuz olan Dünyamız etrafında yörüngesinde dönen Ay’ın dönemlerinden gelir, kozmolojik fenomenlerdir, takvim ile hayatımıza taşınmışlardır.
7 ve 19 sayılarına tam olarak bölünebilme sayısal yapısını matematiksel olarak aşağıdaki denkliklerle ifade etmek mümkündür.
Kur’ân sayısal kodlamasının denklikleri;
≡ 0 (mod 7) ve/veya ≡ 0 (mod 19)
Bu sayısal denklikler, Kur’ân sayısal verisinin (Sure numaraları, Ayet sayıları, kelime sayıları, harf sayıları, bu ve benzer verilerin konumlarını (lokasyonlarını) tanımlayan sayılar, v.b.) 7’e ve/veya 19’a bölündüğünde kalanın sıfır olduğunu veya Kur’ân sayısal verisinin 7’e ve/veya 19’a tam olarak bölündüğünü gösterirler.
Benim çalışmalarım sonucunda, Kur’ân sayısal kodlamasında;
≡ 2 (mod 7) , ≡ 2 (mod 19) , ≡ 7 (mod 19) denkliklerinin de önemli olduğu, kullanılması gerektiği görülmüştür. Kur’ân sayısal verilerinin 7’e ve/veya 19’a bölümlerinin sıfır kalanı verdiğinde sayısal kodlama sistemini doğruladığı gibi, 2 ve 7 kalanları da sayısal kodlama sistemini doğrulamakta, sayısal yapının olağanüstü ve orijinal olduğunu göstermektedir. Benzerliğin ölçülmesi için yapılan Matematiksel modelleme sonucunda ortaya çıkan ≡ 0 (mod 7) , ≡ 0 (mod 19) denkliklerinin, bir zayıf noktası fark edilmiştir. 0 (Sıfır) kalanı veren denklikler, 0 (Sıfır) sayısı girilerek elde edilebilmektedirler. Yani, benzerini getirecek olanlar, zorlandıkları yerlerde 0 (sıfır) sayısal değerini kullanarak sıfır kalanı veren denklikleri kolayca sağlayabilirler, fakat 2 kalanı veren ≡ 2 (mod 7) , ≡ 2 (mod 19) denklikleri sıfır sayısal değerini vererek sağlayamazsınız, mutlaka doğru sayısal değeri bulmanız gerekli olacaktır. İşte bu denklikler benzerlik modellemesinin sıfır sorununu çözen denklikler olarak karşımıza çıkarlar. Denkliklerin nasıl kullanılacağı ilerideki bölümlerde detaylı olarak ele alınmıştır.

Bir yanıt bırakın