
Kur’an benzerliğini ölçmek ve taklit edilemezliğini göstermek için yapılan kodlamalarda üç temel kural (düzen) vardır.
1- Dizilim: Metnin verdiği sıralama esas olarak kabul edilir. Sayılar metnin verdiği sırada alınır. (Düz veya Ters)
2- Bütünsellik: Ölçülen metnin tamamı kapsanmalıdır. Kodlamalarda bütünsellik olmalıdır. (Örüntü gösterilerek bütünsellik ihlal edilebilir)
3- Ölçüt: Ortaya çıkan kodlamalar aynı denklik kümelerinde bulunmalıdırlar.
Bilgisayar Mühendisliği bölümünde yüksek lisans yapan, uluslararası dergilerde makaleleri bulunan bir arkadaşın Youtube videoları altına yapmış olduğu yorumdan çıkardığım soruya cevap verdim:


Soruyu yukarıda verdim, arkadaşımız, heyecanlı heyecanlı, yazmış döktürmüş. Şimdi cevabını verelim.
Öncelikle, Kur’an’daki sayısal yapının nasıl bir mantıkta ortaya çıktığını, neyle karşı karşıya olduğumuzu iyi anlamak lazım. Müsaade ederseniz, bunu bir örnek ile açıklamaya çalışayım.
Hiç Sudoku bulmacası çözdünüz mü? Sudoku bulmacaları gazetelerde, dergilerde görebileceğiniz bir zeka oyunudur. Hemen hemen her yaştan insan tarafından çözülen bir bulmacadır. Farklı boyutları olmakla beraber genellikle, 9 satır ve 9 sütun olmak üzere 81 kareden oluşmaktadır. 81 kare kendi içinde 9 (3×3) kutucuk oluşturur. Hem bu kutucuk içerisindeki 9 kutucuğa hem de satır ve sütunlara 1 den 9 a kadar sayılar yazılır. Kural çok basittir: Hem kutucukta hem de satır ve sütunlarda her rakamdan sadece bir tane olması gerekiyor. Kutucuklar bu kural gözetilerek sayılar ile doldurulur ve soru (bulmaca) çözülür.
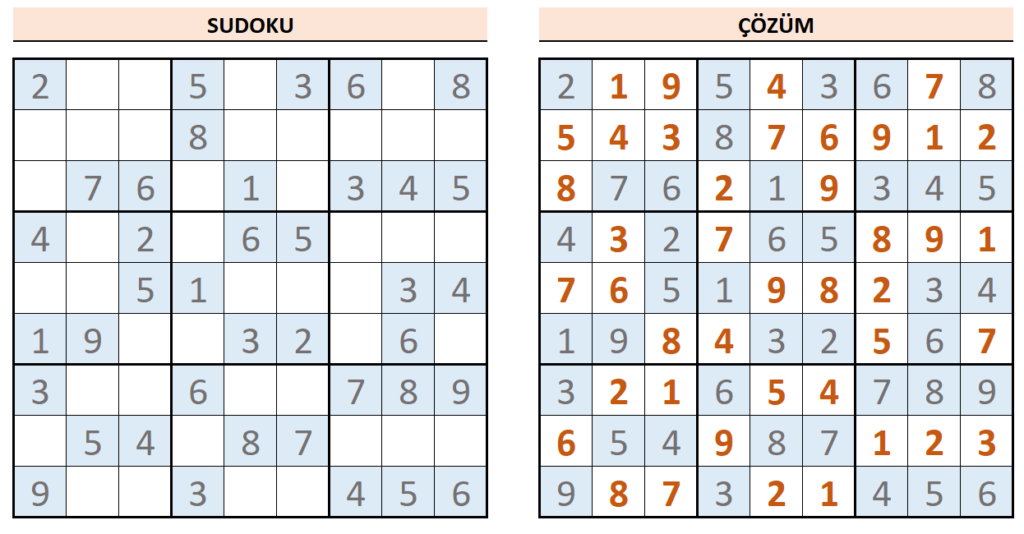
Sudoku bulmacasında matematiksel örüntü ve bu örüntüye bağlı bir sistematik yoktur,
GEREKLİ DEĞİLDİR.
FAKAT KURAL VARDIR.
BULMACAYI DÜZENLEYEN BU KURALA GÖRE DÜZENLER
VE SONRASINDA İSTEDİĞİ SAYILARI ORTAMDAN KALDIRARAK BULMACAYI HAZIRLAR.
BULMACAYI ÇÖZMEYE TALİP KİŞİ
BULMACAYI HAZIRLAYAN KİŞİNİN HANGİ SAYILARI NEDEN KALDIRDIĞINI SORGULAYAMAZ.
Bir Sudoku bulmacası nasıl hazırlanır bilir misiniz? Önce 81 adet kare, hem (3×3)’lük kutucukta hem de satır ve sütunlarda her rakamdan sadece bir tane olacak şekilde 1’den 9’a kadar sayılar ile doldurulur. Bu doldurma işlemi rastgele yapılabilecek bir şey değildir. Sayıların kutucuklara doldurma işlemi çok sakin ve dikkatli yapılması gereken bir iştir. Doldurma esnasında çakışan sayıların, farklı kutucuklara kaydırılması, ayarlanması gerekecektir. Bu şekilde bütün kutucuklar yukarıda verdiğim kural gözetilerek doldurulur. Bulmacayı hazırlayan kişi, öncelikle bulmacanın çözülmüş halini hazırlar. Bütün sayıları yerli yerine koyar ve çözümün nasıl olacağını netleştirir. Böylece bulmacanın çözümünü bilmiş olur. Sonra kutucuklara yazdığı sayılardan istediklerini silerek, sayıların bir çoğunu kutucuklardan kaldırır ve bulmacayı (soruyu) hazırlamış olur. Burada şunu görmek gerekir. Sudoku bulmacasını, yani sorusunu hazırlayan kişi ÇÖZÜMÜ BİLMEKTEDİR, BİLMEK ZORUNDADIR. Çözümünü bilmediğiniz bir Sudoku sorusunu (bulmacasını) ortaya koyamazsınız.
Şimdi soruyorum sizlere:
İnsan, bütün insanların çözemeyeceği
bir Sudoku bulmacasını ortaya koyabilir mi?
Bir Sudoku bulmacasında matematiksel örüntülere bağlı bir sistematiğin olması gerektiği iddia edilebilir mi? Görüldüğü üzere bir Sudoku bulmacasında örüntü ve sistematik yoktur fakat kural, yani düzen vardır. Sudoku bulmacası mantıksal olarak soruların birbirine bağlı olduğu bir yapı değil, cevapların ilişkisi üzerine kurulu bir yapıya (düzene) sahiptir. Soruda veya içindeki küçük kareleri dikkate aldığımızda, sorular arasında matematiksel bir örüntü (düzen) olması gerekli değildir.
Kur’an Sayısal Yapısını, Kur’an korunmuşluğuna dair bir delil olarak göstermek isterseniz, ÖRÜNTÜLÜ KURALLARA ihtiyaç duyarsınız. Kur’an Sayısal Yapısının, Kur’an korunmuşluğuna delil olma özelliği vardır. Kur’an’ın Hafızlık ve Vahiy Katipliği (Tarihi nüshalar) müesseseleri ile korunmuş olduğunu edilgen olarak gösterir, bunun açık bir delilidir. İşte bu delilin ortaya koyulması için matematiksel örüntülere ihtiyaç vardır. Çünkü delil olarak göstermek sayısal yapıya anlam yüklemek demektir. Fakat Kur’an Sayısal Yapısının bundan başka, çok daha önemli olduğunu söyleyebileceğimiz bir özelliği daha vardır, o da Kur’an’ın insanlar tarafından taklit edilemezliğini sağlamaktır. Bu durumda Kur’an Sayısal Yapısına anlamın ötesinde bir işlevsellik yüklenmektedir. Güncel olarak deneyimleyebileceğimiz, nesnel olarak test edebileceğimiz bir işlevsellik. Bu işlevselliğin yine çok ama çok önemli diğer bir sonucu da, Kur’an benzerliğini ölçebileceğimiz bir enstrüman olarak ortaya çıkmasıdır. İşte bu işlevselliğin gerçekleşmesi için MATEMATİKSEL ÖRÜTÜLER İLE TANIMLANAN KURALLARA İHTİYAÇ YOKTUR. Bu ifade etmeye çalıştığım işlevsellik bir SUDOKU bulmacası gibidir. Benzerini yapamayacağınız bir Sudoku bulmacası. Nasıl ki, Sudoku bulmacasında örüntü veya bir sistematik aramak gereksiz ise, aynı şekilde Kur’an Sayısal Yapısının bu özelliğinde de örüntü veya bir sistematik aramak gereksizdir.
Kur’an-ı Kerim’in Sayısal Yapısının bu mantıkta, bu tarz yaklaşımı olan bir sayısal yapı (kodlama – kriptoloji) olduğunu gözlemliyoruz. Karşımızda bir kriptografik bulmaca (kodlama) var, çözüm varyasyonlarını taramaya insanın gücünün yetmeyeceğini hesaplayabildiğimiz, tesadüf olamayacağı için, insanın dışında, çözümü bilen tarafından tasarlanmış olduğunu anladığımız, bütün sorularıyla ve cevaplarıyla önümüzde açık bir şekilde duran, benzerini yapamayacağımız bir kriptografik bulmaca (kodlama)!!? Burada kriptografik bulmacayı (kodlamayı) benzer şekilde farklı sayılar ile çözmemiz (üretmemiz) isteniyor, yani benzerini (dengini-mislini) getirmemiz isteniyor. Benzerini getirebilmemiz için veya benzer bir kriptografik bulmacayı (kodlamayı) hazırlayabilmemiz için çözüm varyasyonlarının tamamını tarayabilmemiz, ÇÖZÜMÜ BİLMEMİZ GEREKİYOR. Bu noktada insan acizliği çok açık gözükmektedir.
25.02.2023 tarihinde yeni eklenen bölüm:
Kodlama matematiksel bir işlem değildir, hedefi matematiksel bir sonuca ulaşmak değildir. Fakat matematiksel yöntemleri kullanarak hedeflenen sonuca ulaşır. Kodlama veya şifreleme her zaman bir bilginin gizlenmesi için kullanılmak zorunda değildir. Günümüzde birçok değişik alanda kodlamanın değişik amaçlar için kullanıldığını görüyoruz. Konuyu anlamanız için Kredi Kartı Numarasının üretilmesinde ve geçerlilik (benzerlik) kontrolünde kullanılan bir kodlama örneğiyle devam edelim.
Kredi Kartlarının üretilmesinde veya geçerliliğinin kontrolünde, bulan kişinin soyadı ile anılan Luhn algoritması kullanılır. Luhn algoritması, Hans Peter Luhn ve IBM tarafından 1954 yılında geliştirilen bir algoritmadır. Aynı zamanda Luhn Check ve Mod Check olarak da isimlendirilmektedir.
Luhn algoritması 2 şekilde kullanılmaktadır.
1. Yeni bir Kredi Kartı Numarası üretmek yani, verilen bir sayıyı Luhn algoritmasına göre hazırlamak,
2. Verilen bir Kredi Kartı Numarasının geçerli olup olmadığını yani, denkliğini (benzerliğini) kontrol etmek.
Aşağıda Luhn algoritmasının 2. fonksiyonu olan; Verilen bir Kredi Kartı Numarasının Luhn algoritmasına göre geçerli (benzer – denk – misli) olup olmadığının nasıl kontrol edildiğini ve kodlama detayını görmeniz mümkündür.
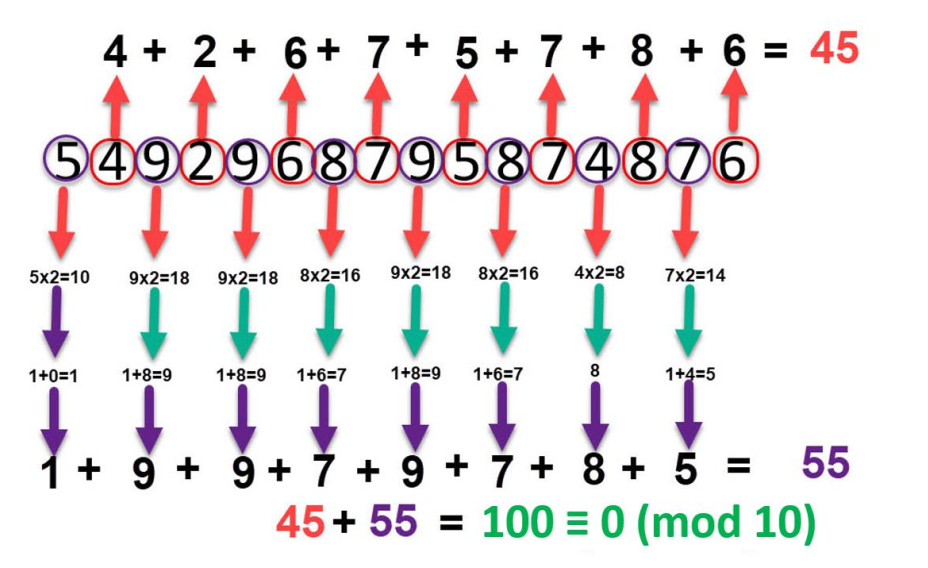
Bu kodlamada, sayılar yan yana yazılmış, belli bir sıradaki sayılar aynı alınmış belli bir diğer sıradaki sayılar 2 sayısı ile çarpılmış ve basamakları toplanarak alınmış ve kodlama üretilmiştir. Geçerlilik kontrolü için ≡ 0 (mod 10) denkliği kullanılıyor. Üretilen kodlamanın bu denkliğin sağlamasıyla, yeni verilmiş olan ve geçerliliği kontrol edilen Kredi Kartı Numarasının Luhn algoritmasıyla üretilen Kredi Kartı Numaraları kümesinin bir elemanı olup olmadığı, yani kümedeki diğer Numaralar ile benzer olup olmadığı tespit edilmiş oluyor. Günümüzde kullanılan tipik bir kodlama örneğidir ve bu kodlamada matematiksel bir örüntüden bahsetmek mümkün değildir, örüntüye ihtiyaç yoktur.
Kur’an’da karşımıza çıkan sayısal yapıya tekrar konsantre olduğumuzda; bu sayısal yapıya (kriptografik bulmacaya – kodlamaya) bir anlam yükleme yaklaşımı, ancak Kur’an korunmuşluğuna delil göstermek istendiğinde gerekli olacaktır. Konuyla ilgilenen bir çok araştırmacıdan farklı olarak, ben bu sayısal yapıya (kriptografik bulmacaya – kodlamaya) bir anlam yüklemek yerine işlevsellik yüklemeyi tercih ediyorum ve Kur’an’ın insanlar tarafından taklit edilemezliğini sağladığını düşünüyorum, görüyorum.
Varyasyonlarını taramaya imkanımızın olmadığını, olasılık değeri olarak hesaplayabildiğimiz, Kur’an’ın doğal sırasında ortaya çıkan ve kriterleri birbirine bağlanan bu sayısal yapıyı, bu bulmacanın çözümünü bilmeyen, bilemeyen bir insanın benzer, yeni bir bulmaca yapabileceğini veya bu bulmacayı uydurarak, yani tesadüf olarak yapabileceğini nasıl söyleyebiliriz?
Çözümü olan ve içinde düzen barındıran
bir karmaşıklığı,
varyasyonlarını taramadan, yani çözümü bilmeden,
insan ortaya koyabilir mi?
Bu bir NEDEN-SONUÇ tanımlaması değildir. Bu bir durum tespitidir. Benzer bir durumu kendi sayılarınızla ortaya çıkaramayacağınız, insanlığın yapamayacağı iddia ediliyor. Yaparım veya Yapılır diyen buyursun. Hodri Meydan. Benzerini getiremezsiniz.
Kur’an Sayısal Yapısında Kriterlerin, kitabın verdiği doğal sıraya göre, sayıların dizilimlerinden oluştuğunu belirtmek isterim. Bu kriterler birbirlerine bağlanarak bir olasılık zinciri oluştururlar ve olasılık değerini astronomik şekilde düşürürler. Bu noktayı kaçırmayınız. Burada bir düzen vardır ve düzeni kitabın kendi doğal yapısı oluşturmaktadır.
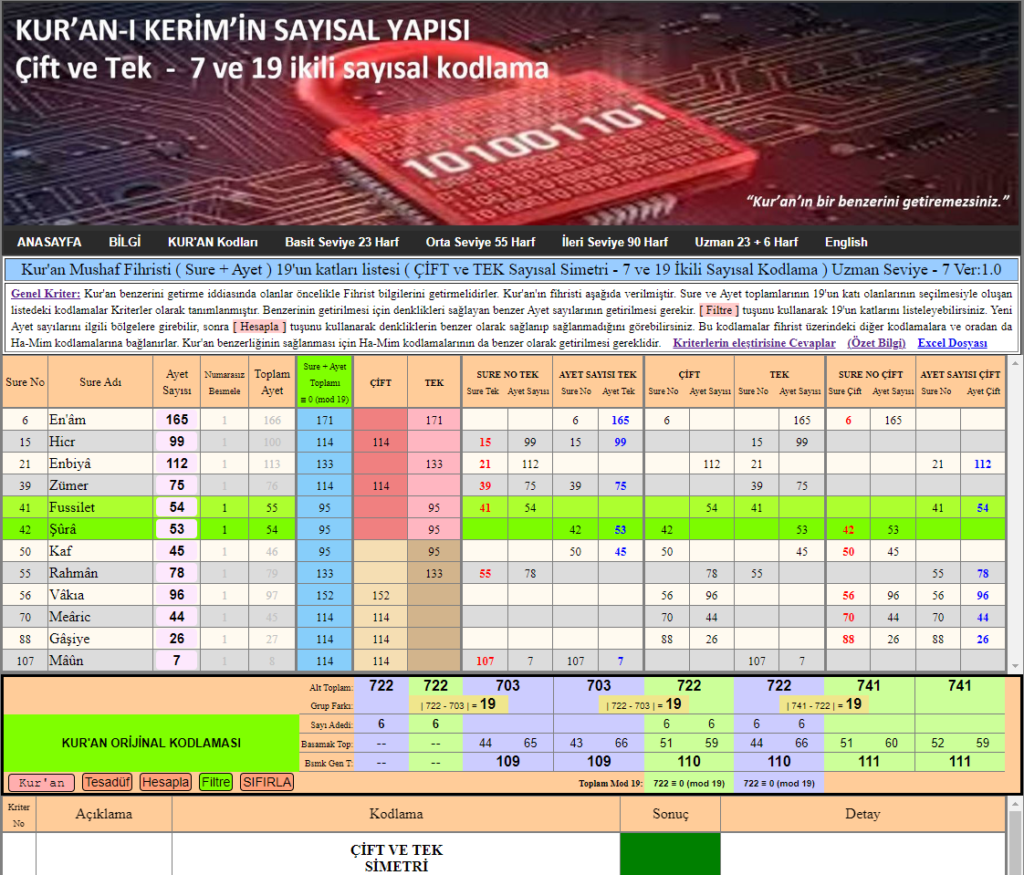
Kitabın verdiği doğal sıralamanın temel kural olması durumunda, kriterlerin birbirlerine bağlanarak oluşturduğu bu olasılık zincirinin, TESADÜFEN oluşabileceğini savunmak mümkün değildir. Çünkü, gözlem ile sabittir. Girin buradan WEB sayfasına, önce listeyi sakin bir şekilde inceleyin, aşağıdaki tabloda bulunan kriterleri anlamaya çalışın, sayısal yapıyı tanıyın. Sonra orada [TESADÜF] tuşunu göreceksiniz. Tesadüf tuşuna basın ve sayıların bilgisayar tarafından rastgele üretilmesini sağlayın,
bu şekilde gözlem ve ölçüm yaparak bu sayısal yapının TESADÜF olamayacağını hemen anlayacaksınız. [ FİLTRE ] tuşunu kapatarak bütün fihristi görebilirsiniz.
Bu sayısal yapı Kur’an’dan alınarak ortaya koyulmuştur. Kur’an’daki 89-Fecr Suresi 3. Ayet – Çift ve Tek kavramları, 74-Müddesir Suresi 30. Ayet – 19 sayısı, 15-Hicr Suresi 87. Ayet – 7 sayısı, bilindiği için bu sayısal yapının Kur’an fihristinde olduğu fark edilebilmiş, çok kısa bir zamanda yapılabilmiş ve ortaya çıkarılmıştır. Benim bu sayısal yapıyı dizayn etmeye kapasitemin yetmediği ortadadır, tesadüf de olamayacağını kendi gözleminiz ve ölçümünüzle rahatlıkla hemen anlayabilirsiniz. Bu durumda bu sayısal yapının nasıl ortaya çıktığını izah etme mecburiyetimiz vardır.!!! Hemen açıkça şunu da söylemek isterim, bu sayısal yapının bir benzerini üretmeye benim gücüm yetmiyor, fakat sizin gücünüz yetiyorsa buyurun bir benzerini hemen yapın görelim. Uyduruyorsunuz (tesadüf) diyenlere Kur’an’ın verdiği cevap budur, bende bu cevabı aynen size iletiyorum.
11. Hud suresi 13. ayet: Yoksa “onu kendi uydurdu” mu diyorlar? O halde sen de onlara de ki: “Haydi siz de onun gibi uydurulmuş on sûre getirin. Allah’dan başka çağırabileceğiniz kim varsa onları da yardıma çağırın. Eğer doğru söylüyorsanız” (bunu yaparsınız).
Yukarıdaki ekran görüntüsünü verdiğim örnekte 12 tane sure bulunmaktadır. Siz bu tabloyu 10 sure getirerek de yapabilirsiniz. Deneyin 10 dk. içinde benzerini getiremeyeceğinizi hemen anlayacaksınız.
Bu şekilde İNSANLARIN YAPAMAYACAĞI BİR SAYISAL YAPI’yı siz veya bir başkası üretebilir mi?
Bunu sakin bir şekilde, iyi düşünün.
Her şey OLASILIK kelimesini iyi anlamakla başlayacaktır. Olasılık; bir şeyin olma, olabilme durumunu ifade eder. Olasılık değeri bir şeyin olma durum sayısının, toplam durum sayısına oranıdır.
Olasılık değeri: Bir şeyin olma durum sayısı / Toplam durum sayısı , yani bütün durumlar içinde kriterlere uygun kaç tane durum oluşuyor, olasılık hesabı bunu gösterir. Mesela; 1/1000 binde bir olasılık deriz.
Kriterlerin birbirlerine bağlanarak oluşturdukları olasılık zincirini aşağıdaki şemadan görebilirsiniz.
Kriterlerin detaylarını ve ilgili videoları bu linkten görebilirsiniz.
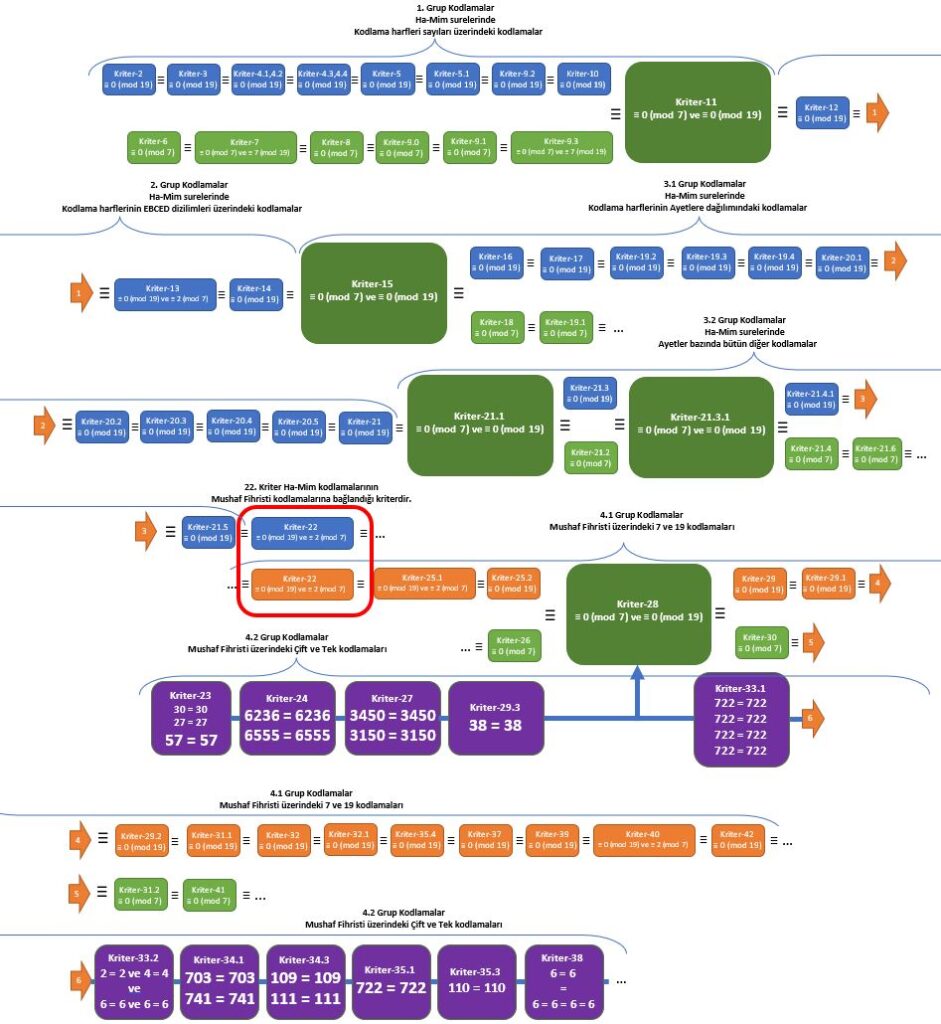
Bu noktada önemli olarak gördüğüm bir matematiksel, mantıksal gerçeği açıklamak gereklidir
Benzeri olmadığı matematiksel olarak görünen bir şeyin,
benzerinin getirilmesi talep edilemez. Mantıklı değildir.
Matematiksel benzerliklerin, yani kriterlerin denklikler olarak tanımlanması gereklidir, eğer bir eşitliği benzerlik ölçütü olarak vermek istiyorsak bu eşitliğin bir oran olarak ortaya koyulması şarttır. Çözüm eğer tek bir sayı veya sayı dizisi olarak karşımıza çıkıyorsa, benzerlik kriteri olarak sunulması mantıklı olmaz. Benzerlik kriteri olarak tanımlanacak eşitliklerin (oranların) veya denkliklerin çözümü mutlaka bir çözüm kümesi olarak karşımıza çıkması gereklidir.
Örnek:

Bu eşitlik bir oran olduğu için benzerlik kriteri olarak sunulabilir, çünkü yukarıdaki eşitlik aynı zamanda bir denkliktir.
8128 sayısı mükemmel sayı olarak nitelendirilir. “Mükemmel sayı, sayılar teorisinde, kendisi hariç pozitif tam bölenlerinin toplamı kendisine eşit olan sayı” şeklinde tanımlanır.
1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128
Yukarıda verilen bir matematiksel eşitliktir. Matematiksel benzerliğinin denklik olarak tanımlanması gerekir. Bu şekilde bir denkliğin tanımlanması mümkün değildir, çünkü dengi yoktur.!!! Çözüm tek bir sayı dizisidir, bir çözüm kümesi olarak karşımıza çıkmaz.
8128 sayısı ile oluşan eşitliği, siz bir kriter olarak sunup, bu matematiksel özelliği barındıran benzer bir sayı getirilmesini talep edemezsiniz. Örnek olarak bir Kriter tanımlamaya çalışalım.
Kriter: Kendisi hariç 13 adet pozitif tam böleni olan ve bölenlerinin toplamı kendisine eşit ve basamak toplamı (8+1+2+8=19) 19 olan sayının benzerini getiriniz.
Bu kriterin benzerlik kümesi boş kümedir, benzeri yoktur, benzerlik olasılığı 1/0’dır. Yani tanımsızdır. Benzerinin getirilmesi talep edilemez. Farkındaysanız, kriter denklik olarak yazılamıyor.
Bu eleştiriyi yapan, 8128 sayısına benzer bir sayı getiremeyeceğimi ifade eden arkadaş, Bilgisayar Müh. Doktora öğrencisi fakat matematiksel benzerliğin ifade edilmesi konusunda yetersiz olduğu çok açık.
Bir sayı dizisinin benzerinin getirilip, getirilemeyeceği, kriterlerinin ortaya koyduğu olasılık değeriyle anlaşılır. Eğer benzerlik olasılığı tanımsız ise, yani benzeri yoksa, benzerinin getirilmesinin talep edilmesi mantıklı değildir. Sayı teorilerinin ortaya koyduğu mükemmel sayılar olarak bilinen sayıları oluşturan sayı dizileri veya Pi sayısı (π), 3,14159… veya Euler’in sayısı (e=2,71828…) gibi transandantal sayıların benzerleri yoktur. Bu benzeri olmayan sayı dizilerinden veya benzeri olmayan sayılardan oluşturulan eşitliklerin benzerlik kriteri olarak tanımlanabilmesi için denklik halinde ifade edilmesi gereklidir. Biraz Matematik bilgisine sahip olanlar, bu tip eşitliklerin denklikler olarak ifade edilemediğini görebilirler. Bu sayıların denklikler olarak değil de, eşitlikler olarak verildiği bir sayısal yapının benzerlik olasılık değeri tanımsızdır, benzerinin getirilmesinin talep edilmesi mantıklı değildir.
Bu noktada Kur’an metni benzerliğinin matematiksel modelleme temel ilkelerinin öncelikle ortaya koyulması gereklidir. Aşağıda benim düşündüğüm temel ilkeleri sıraladım.
Matematiksel Modellemede;
- Kur’an’da var olan bir sayısal yapının ortaya çıkarılması, tespit edilmesi üzerine, metindeki kodlamalar modellenir. Kodlama metnin matematiksel karakteristiğini barındırmalıdır.
- Kodlamalarda Kur’an’ın öne çıkardığı, sayısal yapı ile ilgisi ayetler ile kurulan sayılar ve kavramlar kullanılır.
- Kodlamalarda Kur’an metnindeki doğal sıralama dikkate alınır ve kodlamanın kendi içinde bütünsellik aranır.
- Kodlamalarda Kur’an’ın öne çıkardığı sayılar ve kavramlar ile ortaya çıkan örüntülerde bütünsellik ilkesi ihlal edilebilir.
Kur’an Sayısal Yapısının kriterleri denklikler olarak ortaya koyulmuştur, olasılık değerleri tanımlıdır, mükemmel sayı niteliğinde bir matematiksel özelliğinin olup olmadığını henüz bilemiyorum, fakat tanımlanan kriterlerde böyle bir özellik kriter olarak öne sürülmemiştir, yani benzeri getirilebilir niteliktedir, fakat olasılık değerine baktığımızda, bu olasılığın sağlanacağı varyasyon taramasını yapmak için evrenimizin zamanının yeterli olmadığı anlaşılacaktır.
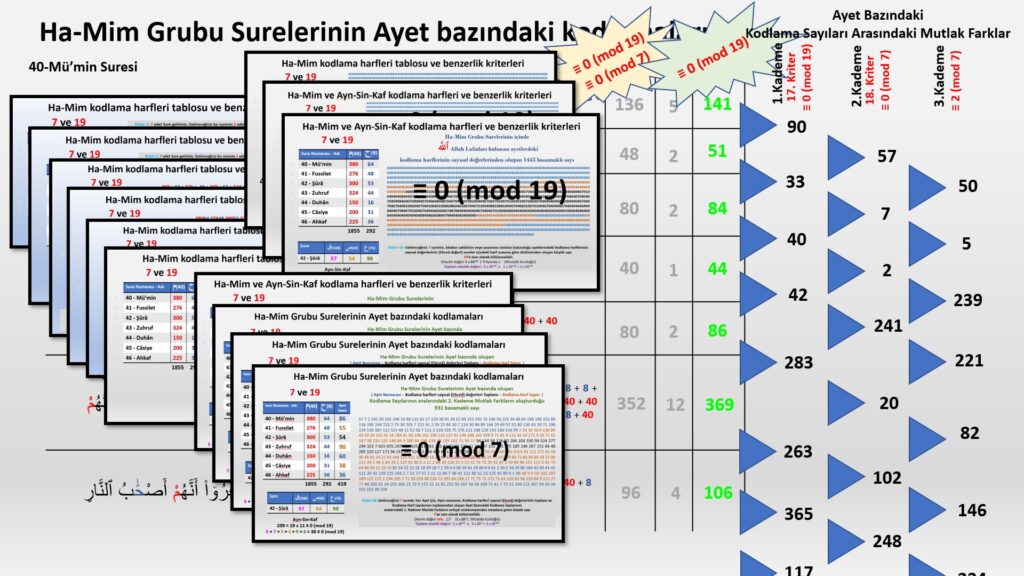
Örnek olarak, yukarıdaki resimde: 5. kriterde satır grupları olan 380 64, 276 48, 300 53, … gibi oluşan sayılar doğal sırasına göre ardışık yazıldığında oluşan 35 basamaklı sayı 19’a tam olarak bölünür.
380 64 276 48 300 53 324 44 150 16 200 31 225 36 ≡ 0 (mod 19)
=19 x 2003382972789754339165798000164344
Satır gruplarının 380 64, 276 48, 300 53, … ,yani 5 basamaklı 7 adet sayının değişik sırayla dizilimlerinden 5040 kombinasyon (7!=5040) oluşabilir ve bu 5040 kombinasyon içinden 253 tanesi 19’a tam olarak bölünebilir. 5. kriteri oluşturan doğal sıralama dizilimine ilave olarak aşağıda, sıralaması doğal sıralamadan farklı olan 5 tane daha 19’a tam olarak bölünen örnek dizilim veriyorum. 19’a tam olarak bölünebilen 253 dizilimden sadece bir tanesi, doğal sırada olanı kriter olarak sunulmuştur. Diğer 19’a tam olarak bölünen 252 dizilim de kriter olarak sunulsaydı varyasyon sayısı astronomik artacak, fakat sıralama şartı olmadığı için verdiğimiz her sayı dizisinde her zaman 253 tane şartı sağlayan dizilim olacağı için matematiksel olarak bir değeri olmayacaktı. Fakat bu şekilde yapılmamıştır. Eğer doğal sırada olan dizilim 19’a tam olarak bölünmeseydi bu dizilim kriter olarak sunulamayacaktı. Dolayısıyla doğal sıralama, oluşan sayısal yapıyı sınırlandırır, olasılığı düşürür, istatistiksel bir değer kazandırır ve doğal bir düzen sağlar. Sayı dizilimlerinin keyfi, aranan kriterlere uygun olarak seçildiği iddia edilemez. Doğal sıralama varyasyonları sınırlar, bir düzen, kural koyar, varyasyon sayısının çok büyük değerlere ulaşmasını çok ciddi şekilde kısıtlar. Bundan dolayıdır ki, sayısal yapı kendine has bir özellik kazanmaya başlar, metnin matematiksel karakteristiğini yansıtır ve aynı zamanda benzerinin yapılması zorlaşır.
380 64 276 48 300 53 200 31 324 44 150 16 225 36 ≡ 0 (mod 19)
=19 x 2003382972789753685859181131664344
380 64 276 48 324 44 225 36 150 16 300 53 200 31 ≡ 0 (mod 19)
=19 x 2003382972802338028218429631858949
380 64 276 48 150 16 225 36 300 53 324 44 200 31 ≡ 0 (mod 19)
=19 x 2003382972710611712436870170758949
380 64 276 48 200 31 300 53 324 44 225 36 150 16 ≡ 0 (mod 19)
=19 x 2003382972737006844911812750190264
380 64 276 48 200 31 225 36 324 44 150 16 300 53 ≡ 0 (mod 19)
=19 x 2003382972737006449280233763243687
İstatistik biliminin bize gösterdiği çok açık bir sonuç vardır; Tanımlanan kuralların kısıtladığı durumlar arasından, ortaya çıkan olasılık yoğunluğu bölgesinin dışındaki bir durum, beklenmeyen, olağanüstü bir durum olarak nitelendirilir. Eğer tanımlanmış bütün durumların sayısı deneme imkânımızın ötesine geçiyorsa, ortaya çıkan olasılık yoğunluğu bölgesinin dışındaki bu durumun insanlar tarafından yapılamayacağını söyleyebiliriz.
Bu doğal sıralama olarak tanımlanan kural, kitabın koyduğu düzen, kodlama harflerinin sureler içindeki dizilimlerinden oluşan kodlamalarda ve yine, kodlama harflerinin ayetlere dağılımından oluşan kodlamalarda, yani 12. kriter ve sonrasında, daha açık bir şekilde kendini göstermektedir. Aşağıda linklerini verdiğim bu kriterleri detaylı olarak incelemenizi öneriyorum. Bu kodlamaların oluşumunda keyfi bir yaklaşım olduğunu ileri sürmek veya rastgele bir oluşum olduğunu söylemek veya benzerini getireceğini iddia etmek akıl sahibi bir insan için imkansız gözükmektedir.
Örüntü arayışı, yani extra bir sistematik arayışı, insanların dışarıdan kurallar koymaları gerekli değildir.
Ölçütler 7 ve 19, ikililerden(2), Çift ve Tek olarak Kur’an tarafından ayetlerde zikredilerek belirlenmiş ve kurallar, Kur’an’ın vermiş olduğu doğal sıra olacak şekilde Kur’an tarafından koyulmuştur.
Kur’an sayısal yapısında sistematik, kriterler kullanılarak cevapların ilişkileri üzerine kurgulanmıştır ve cevaplar açıktır, kriterler belirlenmiştir.
Sorular arasında mantıksal bağlantılar (Örüntüler) tanımlamak gerekli değildir.
Detaylı bilgi almak için ilgili yazımı okuyunuz.
(trurthsearcher 361) Doğruyu arayan kardeşim, uzmanlığınız var. Öyleyse, kriterleri sağlayan sayıların benzerini getirebilirsiniz. Kur’an örneğini ve benim yaptığım örneği aşağıya yazıyorum. Uzmanlığınızı kullanın ve benzer bir sayı dizisi de siz getirin.
Önce müsaadenizle kısa bir açıklama yapmak istiyorum.
Teknik adama, uzmanlığı olan adama, konu hakkında bu şekilde ileri geri yorum yapmak yakışmıyor. İddia bellidir. Benzerini getiremezsiniz deniyor. Benzerini getirebiliyorsanız getirin, benzerini getiremiyorsanız size susmak kalır. (Bu şekilde her yazının bir benzeri getirilemez demekle işin içinden çıkamazsınız, sizde kendi oluşturduğunuz örneği getirin o zaman)
Fakat bende başka bir örnek sayı dizisi getiririm sizde onun benzerini getiremezsiniz diyorsanız, bu başka bir iddia olur. Öncelikle getireceğiniz bu sayı dizisinin kriterlerinin olasılık hesabını göstermelisiniz. Olasılık hesabını gösteremiyorsanız dikkate alabileceğimiz hiç bir iddianız kalmaz. Konu kapanmış olur. Benzerlik kriterlerinin olasılık hesabı tanımsız olmamalıdır, belli bir olasılık değerine sahip olmalıdır. Bu durumda, iddianızın kendi içinde tutarsız olduğu çok basit bir şekilde ortaya koyulabilir. Şimdi siz düşünerek, olasılık hesabını yaparak, planlayarak, denemeler yaparak bir sayı dizisi getiriyorsunuz, bütün gereklilikleri, yani kriterlerinizi açıklıyorsunuz, siz insansınız bunu yapıyorsunuz ve başka bir insanın yapamayacağını, bu olasılık değerine siz ulaştığınız halde başkasının ulaşamayacağını iddia ediyorsunuz. Bir kere siz insansınız, insanın yapamayacağını söylemeniz sizi zaten baştan çelişkiye düşürüyor. Benim durumum bu noktada çok büyük farklılık gösteriyor, ben Kur’an’dan alarak ortaya koyuyorum sayısal yapıyı, tasarım bana ait değil, ben bir şeyi düşünmüyorum, tasarlamıyorum, olasılık varyasyonlarını taramıyorum, zaten tarayamam buna zamanım yetmeyeceğini hesaplayabiliyoruz, yani hazır olanı bulup ortaya çıkarıyorum. Tasarım gücü bana ait değil. Durum çok farklı, neyse siz yine de getirin sayı dizisini bakalım, benzerini getirebiliyor muyuz, getiremiyor muyuz, görelim. Madem Uluslararası düzeyde makaleleriniz var, madem Bilgisayar Mühendisliği Lisansınız var.
BUYURUN HODRİ MEYDAN. BENDE KAFA TUTACAK, YAPARIM DİYECEK ADAM ARIYORDUM ZATEN.
Bence kaçırdığınız çok şey var. Maddeler halinde sıralıyorum.
1- Kriter olarak kullanılan sayılar Kur’an ayetlerinde konuyla, anlam olarak irtibatı bulunan sayılardır. Önce sayısal yapı incelenmiş, kodlama elementleri bölünmüş, araştırma yapılmış ve uygun olduğu için bu sayılar seçilmiş değildir!!!… Hangi rastgele sayı seçiminden bahsediyorsunuz, ne dediğinizi biliyor musunuz, duyuyor musunuz?
7 ve 19 , ikililerden (2), Çift ve Tek
15-Hicr Suresi 87. Ayet – 74-Müddesir Suresi 30. Ayet – 89-Fecr Suresi 3. Ayet
2- Sureler grubu 1. ayetleri özellikle belirtilmiş Ha ve Mim harflerinden oluşur. Sureler grubu gelişi güzel seçilmemiştir, doğal oluşumuna göre, doğal sırasına göre alınmıştır.
3- Bütün kriterlerdeki sayı dizilimleri doğal sırasındadır. Veya doğal ters sırasındadır. Doğal olmayan bir sayı dizilimi seçilmemiştir. Sizin belirttiğiniz gibi, keyfi bir seçim yoktur.
Bu seçimi keyfi olarak zaten yapamazsınız.
Siz, ben yaparım benzerini veya başka bir örneğini diyorsanız HODRİ MEYDAN. Yapın görelim.
Bu noktada, Bilgisayar Mühendisi Doktora öğrencisi olduğunu söyleyen Kaan Oz’a, Sn. Bülend Sungur’un cevabı çok kıymetli, arşivlenecek bir cevap. Paylaşıyorum, mutlaka okuyunuz.
Bülend Sungur (Tweet)
Kaan Bey kardeşim, “benzerini insanların getiremeyeceği bir seri getirmek” suretiyle Sn. Kurdoğlu’nun tezinin çürütülmesi mümkün değil!
TEZ ve soru şu: İlâhî metnin/mesajın SÖZEL yapısına/anlam dünyasına muhatap ve Kurân’ın MUCİZE olduğuna iman etmiş müminler olarak, TEHADDÎ âyetlerinin meydan okumasını nasıl yapıp ederek TEST edilebilir/ölçümlenebilir kılarız?!
İşte burada HURUFUMUKATTAA’lardan hareketle HA-MÎM sûreleri özelinde/örneğinde sözel olanın sayısal olana tahvili ile ortaya çıkan bir matematik iskelet/tasarım var. Bu tasarımın sathı SÖZEL, “sırtı/arkası” sayısal olduğuna göre, TEHADDÎ âyetlerinin meydan okumasını kabul edenlerin ÖNCE sözel bir yetkinlik ortaya koymaları ve o yetkinliğin metnini sayısal bir tasarımla da desteklemeleri gerekmektedir. Bu yapılabilirse (!) ilâhî metinle onun benzeri olmak iddiasındaki diğer metnin -sahip oldukları sayısal tasarım/ölçek itibariyle- mukayesesi ve İLÂHÎ metnin MUCİZE, diğer metnin ise ACUZE olduğu HESAP edilebilir/görülebilir.
Hülasa, bu satırları başkalarının da okuyacağını hesap ederek şöyle toparlamak isterim. Sn. Kurdoğlu, bizzat benimle yazışmalarında matematik ölçekte BENZERSİZ olmakla BENZERİNİ GETİRMENİN ins-ü-cin takatini aşmaklığının farkına işaret etmiştir. Zâten, bu ifade/argüman/ibare -kanaatimce- ancak sayısal düzlemde geçerli olabilecek/ölçülebilecek bir nüanstır. Yoksa, LİSAN/EDEBİYAT düzleminde bir şeyin benzerini getirmenin zorluğu onu BENZERSİZ kılar. Yani, SÖZEL olanda/alanda böyle bir ayırım yoktur. Şu halde, değerli araştırmacı TAM OLARAK ne demiş oluyor bize/herkese?!
Gelin, TEHADDÎ âyetlerinin hükmünü cârî/merî kılacak ve bunu sözel alanın kısıtlarından kurtaracak, herkesin kabul edeceği bir KIST/KISTAS olan EVRENSEL DİL matematik ile yapalım…
Eğer, TEHADDÎ âyetlerinin meydan okumasına karşılık vereceklerin, verdikleri karşılığın ölçümü hususunda siz daha nesnel bir modele/teze sahipseniz, Kurân İ’CÂZ araştırmalarına katkı vermiş olursunuz. Değilseniz; Sn. Kurdoğlu’nun katkısı önemlidir.
Kaan Oz (Tweet)
Selam Bülend bey,
Siz beni anlamadınız sanırım. Her seri özeldir hiçbir serinin benzeri getirilemez. Herhangi bir metni alın. Sayılara çevirin. Sonra o sayılar üzerinden modlarını alın benim yaptığım gibi yanyana getirin bölün çıkarın farklı kombinasyonlar uydurun. 50 tane kriter uydurun sayıların tüm matematiksel kimliğini çıkarın. Bu sayılarda başka hiçbir sayıda olmayan özellikler çıkardıktan sonra bu yöntemle herhangi bir metin mucize çıkacaktır.
Bu ateistler için harika bir dalga konusu olmak dışında bir işimize yaramaz malesef. Eğer mustafa bey ünlü biri olsaydı efe aydal veya onun gibi bir ateist tonton ve arkadaşları kitabını alıp sayılara çevirip bunu yapıp işte sizin mucizenizde kitabınızda bu diyebilirdi. Komik durumlara düşmemek için matematiğe saygı duymalıyız diye düşünüyorum. Her sayıda olan benzersizlik özelliğini sanki yeni bir keşifmiş gibi sunmak bir matematikçi açısından ne kadar ciddiye alınabilir. Düşünün lütfen. Çalışmada hiçbir sistem yok. Hiçbir örgü yok. Tutarlılık yok lütfen eğer samimiyseniz yaptığım eleştirileri okuyunuz. Selamlar.
Bülend Sungur (Tweet)
Ateistler için her şey dalga konusudur. Onların MİZAH anlayışının bizim için hiçbir hükmü yok. Sizi çok iyi anladığım için sualim şudur.
TEHADDÎ âyetlerinin vurguladığı bir ya da birkaç sûrenin benzerini getirmek hususunda sizin bir ÖLÇÜM önermeniz var mıdır?
Misal, sizi tanımadığım için soruyorum? Siz bu anlayışınızla Kurân’ın 19’cul bir simetrisinin bulunmadığını mı düşünüyorsunuz? Bulunuyor olsa bile bunun benzerinin getirilebileceğini yani MUCİZE olmadığını mı düşünüyorsunuz? Hayır; MUCİZEdir diyorsanız; o ateistlere sayısal bir KRİTER “uydurmuş” olmuyor musunuz?! O ateistler size 19 yerine 18’i kriter belirleyerek gelirlerse, sizdeki 19’cul tasarımla onlardaki 18’cil tasarımın benzerliğine ve hangisinin mucize hangisinin acuze olduğuna kim/nasıl karar verecek?
TEŞEKKÜRLER BÜLEND BEY, ALLAH RAZI OLSUN
Bu muhteşem cevaplar konuyu çok iyi bir şekilde izah etmiş durumdadır. Ben yazıma devam ediyorum ve Kaan Oz’a cevap vermeye devam ediyorum.
Ben yaptım konuşuyorum. Siz yapmadınız konuşma hakkına sahip değilsiniz. Yapın ve sizde konuşma hakkına sahip olun. Yani metinde, özel olarak belirtilmiş harflerin sayıları, dizilimleri ve ayetlere dağılımında bu matematiksel özellikler olmasaydı bu denklik bağlantılarını oluşturamazdık. Bunların benim tarafımdan uydurulduğunu eğer söylüyorsanız. Açıkça soruyorum. Benim uydurduğum şeyin benzerini siz neden uyduramayasınız? Aşağıda 50 kriterin ilk 11+3 (14) tanesini verdim. Bu 14 kriterin varyasyon sayısı 44 Kentilyon’da 1 dir. 1 / ( 44 x 10+18 ). 8Gz hızındaki bir bilgisayar ile saniyede 50.000 varyasyon tarayabildiğimi hesapladım. Bu hesaba göre 44 Kentilyon’da 1 olan bu ihtimali benim bilgisayarım doğal iterasyonla 28 Milyon yılda bulabilecek. Siz bilgisayar mühendisi olduğunuza göre daha hızlı bilgisayarınız veya bilgisayarlarınız ve daha sofistike algoritmalarınız vardır. Belki siz daha kısa zamanda bulabilirsiniz bu kriterleri sağlayan benzer bir sayısal kodlamayı, bekliyoruz cevabınızı.
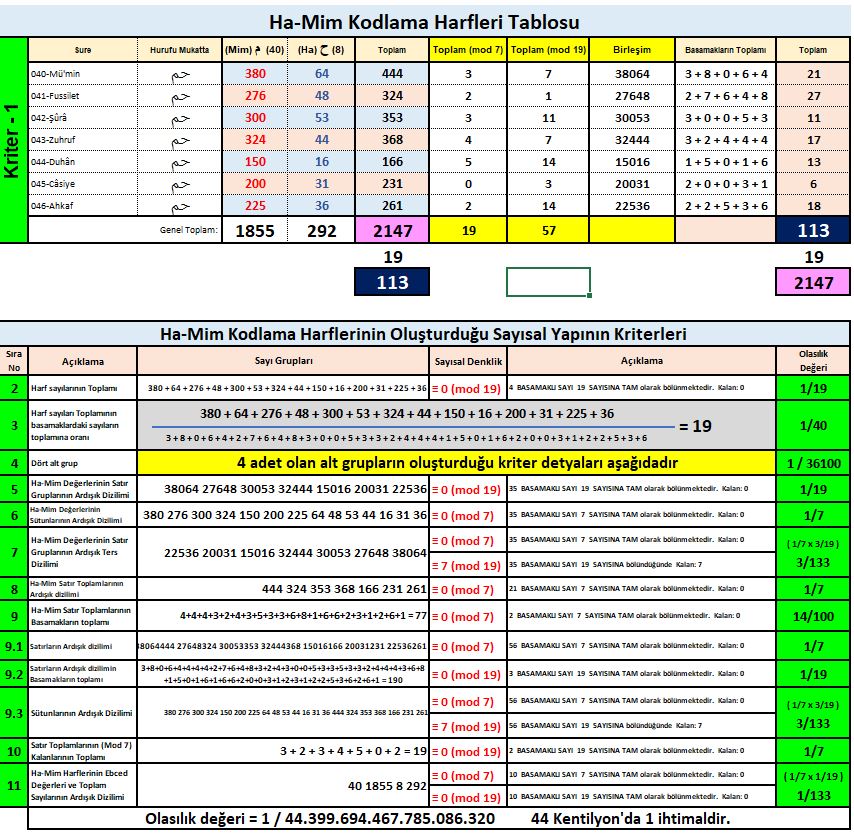
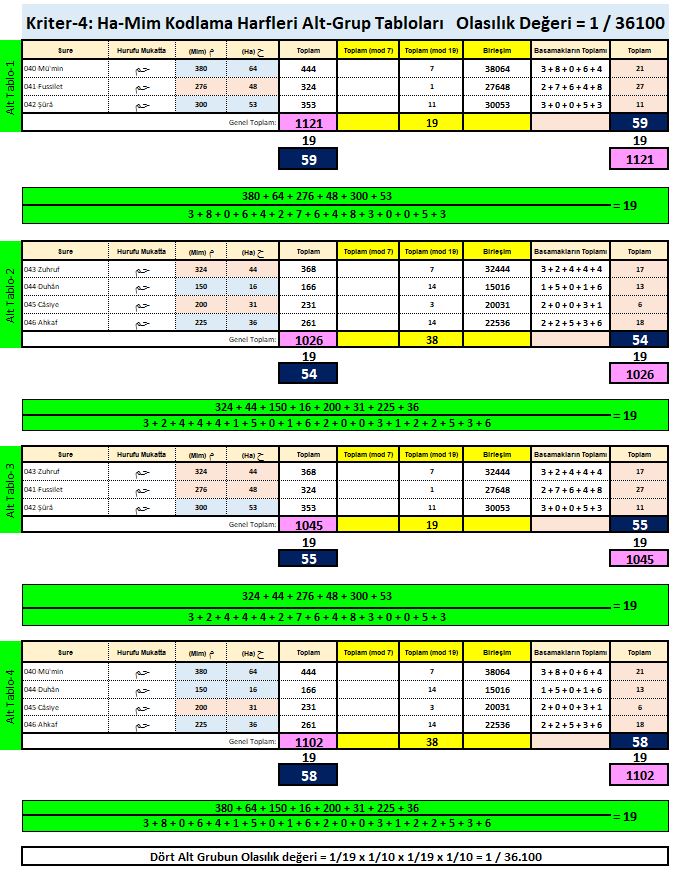
Madem ben uyduruyorum, o zaman insanlar yapabilmeliler değil mi?!!!
Ha-Mim Tablosunu buradan Excel dosyası olarak indirebilirsiniz
Verdiğim sayısal yapıda veya metindeki harflerin oluşturduğu sayısal yapıda sanki hiç bir kural yokmuş gibi, konuyu sunuyorsunuz, algılıyorsunuz. Hayır, bu yaklaşımınız doğru değil. Tekrar yazıyorum. Bütün kriterler, sayı dizilimleri, bütün kodlamalar metindeki doğal haliyle oluşturulmuşlardır. Zorlamalı bir dizilim veya sayı dizilimlerinde doğal olmayan bir yer değişikliği yapılmamıştır. Bunu benim sizin gibi bir uzmana detaylı açıklamama bile gerek yok.
Bu noktada ayıp ediyorsunuz. Lütfen biraz daha olaya itina gösterin. Çalışmayı çok hafife alıyorsunuz. Bugüne kadar dediğimiz, 1 senelik bir olaydır, ben yurtdışında olduğum için maalesef üniversitelere götürme imkanım olmadı konuyu. Konuyu üniversitelerdeki akademisyenlere taşıdığımda, olayın nasıl bir boyut aldığını göreceksiniz. Ben mesela akademisyen olsaydım, bana böyle bir kodlama getirilseydi, çok ciddi varyasyon yapısını inceler, olasılık hesabını yapardım.
Doğruyu arayan kardeşim, Yazdıklarınızı bir daha değerlendirdim. Gerçekten çok büyük haksızlık yaptığınızı gördüm. Size uzun yazmama gerek olduğunu zannetmiyorum, sizin uzmanlığınız bu konuda, dolayısıyla çok kolay anlayabilirsiniz. Ha-Mim gurubunda oluşan 4002 basamaklı sayısal kodlama (12. kriter) ile bu kodlamaya Ayn-Sin-Kaf harflerinin eklenmesiyle oluşan ikinci önemli 4475 basamaklı sayısal kodlamanın (13. kriter) yapısını incelemenizi özellikle istirham ediyorum. Bu sayısal yapının benim tarafımdan uydurulduğunu mu düşünüyorsunuz. Lütfen arkadaşım, bari uzman olarak siz söylemeyin. Önemsiz olduğunu, uydurulmuş olduğunu, rastgele oluşabileceğini lütfen siz söylemeyin bari, bir uzman olarak. 1400 sene önce çöl kumlarının arasında yazılan bir kitapta….. LÜTFEN NE DEDİĞİNİZİ BİR DAHA DÜŞÜNÜN.
Bilimi ve bilimsel düşünceyi bu kadar kirletmenize müsaade etmek, mazluma, bilmeyen insanlara, bilgiye ihtiyaç duyan insanlara zulüm olur. Buna müsaade edemeyeceğim.
Denemesi çok basit; Sayıları ve birbirine zincir şeklinde bağlı olan 50 matematiksel özelliğinden ilk 3 özelliğini aşağıda veriyorum, kendini denemek isteyen denesin.
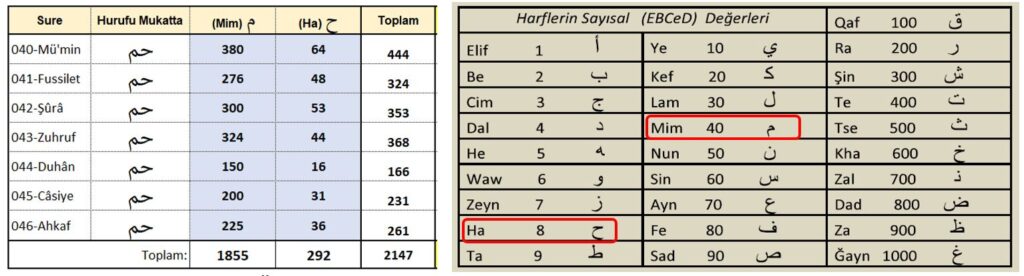
Sayı dizisi 7 adet 3 basamaklı ve 2 basamaklı sayılardan oluşur.
Bu sayılar Kur’an’daki Ha-Mim Surelerindeki Ha ve Mim harflerinin sayılarıdır.
Sayıların toplamı 19’a tam olarak bölünür.
380 + 64 + 276 + 48 + 300 + 53 + 324 + 44 + 150 + 16 + 200 + 31 + 225 + 36 ≡ 0 (mod 19)
Kodlama harflerinin toplamının,
harf sayılarının basamaklarındaki sayıların toplamına
bölümü (oranı) 19’a eşit olmalıdır.
380 + 64 + 276 + 48 + 300 + 53 + 324 + 44 + 150 + 16 + 200 + 31 + 225 + 36
——————————————————————————————————————————————— = 19
3+8+0 + 6+4 + 2+7+6 + 4+8 + 3+0+0 + 5+3 + 3+2+4 + 4+4 + 1+5+0 + 1+6 + 2+0+0 + 3+1 + 2+2+5 + 3+6
Sayı dizisi İki ayrı gruba ayrıldığında da aynı sistematik çalışır.
380 + 64 + 276 + 48 + 300 + 53
————————————————————————- = 19
3+8+0 + 6+4 + 2+7+6 + 4+8 + 3+0+0 + 5+3
324 + 44 + 150 + 16 + 200 + 31 + 225 + 36
—————————————————————————– = 19
3+2+4 + 4+4 + 1+5+0 + 1+6 + 2+0+0 + 3+1 + 2+2+5 + 3+6
İkiye ayrılan grupların ilk sayı grupları (3 basamaklı ve 2 basamaklı)
kendi içinde yer değiştirildiğinde de aynı sistematik çalışır.
324 + 44 + 276 + 48 + 300 + 53
————————————————————————- = 19
3+2+4 + 4+4 + 2+7+6 + 4+8 + 3+0+0 + 5+3
380 + 64 + 150 + 16 + 200 + 31 + 225 + 36
—————————————————————————– = 19
3+8+0 + 6+4 + 1+5+0 + 1+6 + 2+0+0 + 3+1 + 2+2+5 + 3+6
Sayıların toplamının,
basamaklarındaki sayıların toplamına
bölümü (oranı) 19’a eşit olacak şekilde
3’lü ve 4’lü gruplar halinde dört alt grubu olmalıdır.
Sayılar doğal sırasına göre ardışık yazıldığında oluşan 35 basamaklı sayı 19’a tam olarak bölünür.
380 64 276 48 300 53 324 44 150 16 200 31 225 36 ≡ 0 (mod 19)
=19 x 2003382972789754339165798000164344
Kodlama harf sayılarının oluşturduğu tablonun satır gruplarının sırasıyla ardışık dizilimi
19’a tam olarak bölünmelidir.
35 basamaklı sayının 19’a tam olarak bölündüğünü web adresinden kontrol edebilirsiniz
https://goodcalculators.com/big-number-calculator/
Yukardaki sayı gruplarını inceleyiniz,
Ha-Mim Surelerindeki Ha ve Mim Harflerinin sayılarından oluşur. Yukarıdaki sayısal düzeni oluşturmak için, yaklaşık olarak 513 Milyon varyasyonu taramanız gerekir. Şimdilik size bu kadar yeter …
Kolay, bende yaparım diyorsanız, buyurun yapın. Buradan başlayın, sonra devamını yapmak isterseniz videoları izleyin.
Bakalım nereye kadar yapabileceksiniz.
“Nasıl olsa bu sayısal yapı 1400 sene önce insan tarafından yapıldı” diyorsanız, şimdi sizin bilgisayarlarınız da var, avantajlarınız çok fazla. Yapın bakalım yapabiliyorsanız.
Bakın konuyu daha iyi anlayabilmeniz için kendi yaptığım benzer bir sayı grubunu paylaşıyorum, yapmanız gereken böyle bir şey. Öncelikle, getireceğiniz sayıların büyük bir çoğunluğu Kur’an örneğindeki sayılardan farklı olmalı. Yani, yeni sayılar, size özgü sayılar olmalı.
240 + 71 + 230 + 94 + 260 + 93 + 307 + 61 + 219 + 80 + 291 + 41 + 308 + 42 ≡ 0 (mod 19)
Benim örnek olarak verdiğim sayılar yukarıdaki denklikleri sağlıyorlar.
240 + 71 + 230 + 94 + 260 + 93 + 307 + 61 + 219 + 80 + 291 + 41 + 308 + 42
——————————————————————————————————————————————– = 19
2+4+0 + 7+1 + 2+3+0 + 9+4 + 2+6+0 + 9+3 + 3+0+7 + 6+1 + 2+1+9 + 8+0 + 2+9+1 + 4+1 + 3+0+8 + 4+2
Sayı grupları 3 basamaklı ve 2 basamaklı sayılardan oluşur. İki ayrı gruba ayrıldığında da aynı sistematik çalışır.
240 + 71 + 230 + 94 + 260 + 93
————————————————————– = 19
2+4+0 + 7+1 + 2+3+0 + 9+4 + 2+6+0 + 9+3
307 + 61 + 219 + 80 + 291 + 41 + 308 + 42
——————————————————————————— = 19
3+0+7 + 6+1 + 2+1+9 + 8+0 + 2+9+1 + 4+1 + 3+0+8 + 4+2
İkiye ayrılan grubun ilk sayı grupları (3 basamaklı ve 2 basamaklı) kendi içinde yer değiştirildiğinde de aynı sistematik çalışır.
307 + 61 + 230 + 94 + 260 + 93
————————————————————– = 19
3+0+7 + 6+1 + 2+3+0 + 9+4 + 2+6+0 + 9+3
240 + 71 + 219 + 80 + 291 + 41 + 308 + 42
——————————————————————————— = 19
2+4+0 + 7+1 + 2+1+9 + 8+0 + 2+9+1 + 4+1 + 3+0+8 + 4+2
Sayılar ardışık yazıldığında oluşan 35 basamaklı sayı 19’a tam olarak bölünüyor.
240 71 230 94 260 93 307 61 219 80 291 41 308 42 ≡ 0 (mod 19)
“Deneme Tablosu” sayfasında kendi sayılarınızı deneyebilirsiniz.
Evet işte böyle bir örnek getirmeye çalışın, konuyu hemen anlayacaksınız. Nasıl bir şeyden söz ediyoruz. Nasıl bir düzen ile karşı karşıyayız, nasıl bir matematiksel zorluk var ortada. Anlayınca konuya bakış açınız ve fikriniz değişecektir.
Matematiğin gücünü çoğu insan maalesef üstel sayıları algılayamadığı için doğru değerlendiremiyor. Aşağıdaki resimde örnek olarak tasarlanmış büyüklüğünü izah dahi edemeyeceğimiz bir bilgiişlem sisteminin dehşet büyüklükteki varyasyon tarama kapasitesini görebilirsiniz. 100 basamaklı bir sayı grubu içinden her hangi bir sayıyı yazmak 2 dakikamızı alır, fakat bu sayıyı bulmak için bütün varyasyonları taramaya Evrenlerin ömrü yetmez. Kur’an’ın insanlar tarafından taklit edilemezliği neden matematikle ilgilidir, işte buradan çok iyi anlayabilirsiniz.
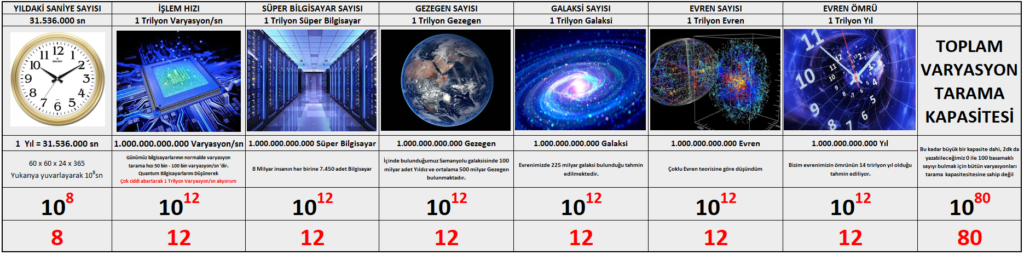







Bir yanıt bırakın